Lagrangepunkter och corioliseffekten

Här blandar vi både stort och smått. Följ med på en lite avancerad, men ändå inte helt obegriplig resa i tyngdlöshet, högt ovanför Jorden. Och för den som undrar om man verkligen har någon nytta av att förstå corioliseffekten, eller ens veta om att den finns så svarar Anders: ”-Gör jag bättre prognoser om jag förstår corioliskraften?

Svaret är detsamma som om du är fotbollskommentator. Att du förstår off-side regeln innebär inte automatiskt att du vet vad som ska hända om 5 sekunder, men det gör dig i stånd att förstå vad som utspelar sig på plan.” /Martin

Av Anders Persson: Svar till Solvid som skrev bl,a.:”Kanske kan vi då även utvidga Coriolis-krafterna till makrokosmos?” …Ja, corioliseffekterna återkommer i olika skepnader om och om igen. Till varje planet i solsystemet finns det fem s.k. Lagrangepunkter (L1,L2, L3, L4 och L5). Ett objekt placerat där följer med jorden i dess bana på ett fixt avstånd.

L1 och L2 ligger strax utanför och innanför jorden på en linje från solen. L3 ligger i jordbanan bakom solen, så den kan inte ses. Dessa tre lagrangepunkter är instabila vilket innebär att det objekt man placerar där, t.ex.en satellit (som man gjort i L1 och/eller L2) tenderar att glida bort och måste varannan vecka ”knuffas” tillbaka på plats.

Att L3 är instabil bevisar att någon s.k.”Planeten X” bakom solen, där alla flygande tefat skulle ha sin hemort, inte kan existera.

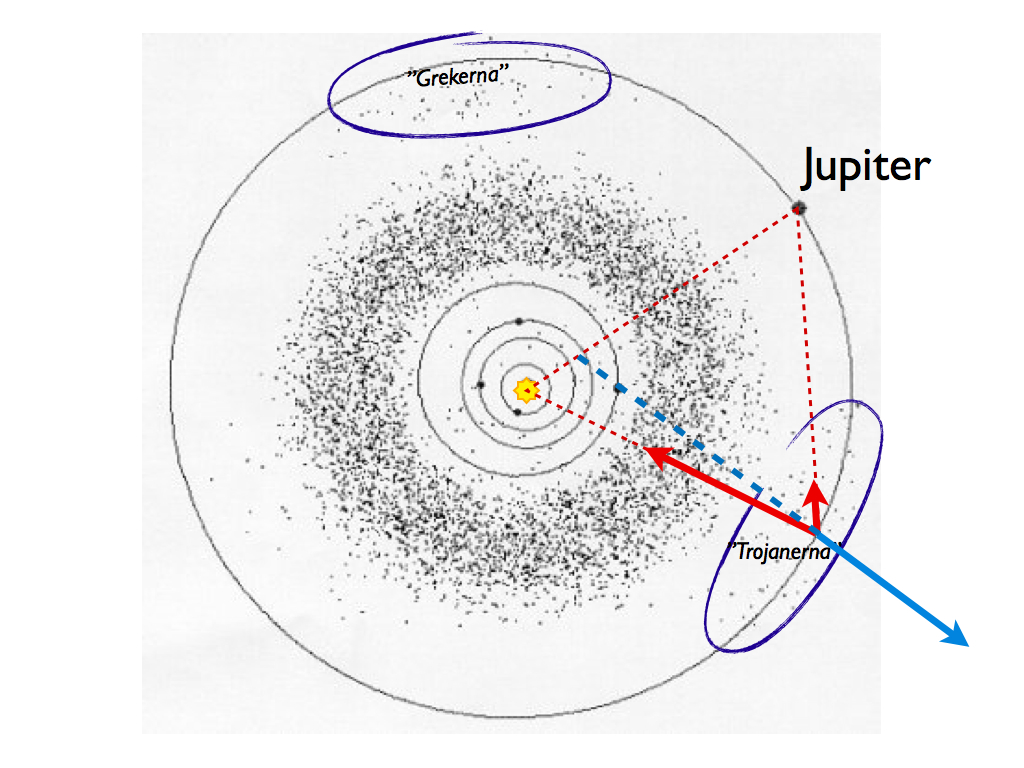
L4 och L5 ligger också i planetbanan men 60 grader före och efter planeten. Dessa punkter är stabila, dvs. varje objekt som hamnar där har svårt att ta sig därifrån. Jupiters L4 och L5 är därför samlingsplatsen för 100-tals små asterioder, ”Grekerna” framför Jupiter, ”Trojanerna” bakom.

Nyligen har man hittat en 300 m stor asteriod som ligger i en av jordens lagrangepunkter. Den heter 2010TK7 och ligger 60 grader före jorden, dvs den är en ”grekisk” asteroid (L4), jagad av ”trojaner” som ännu återstår att upptäcka.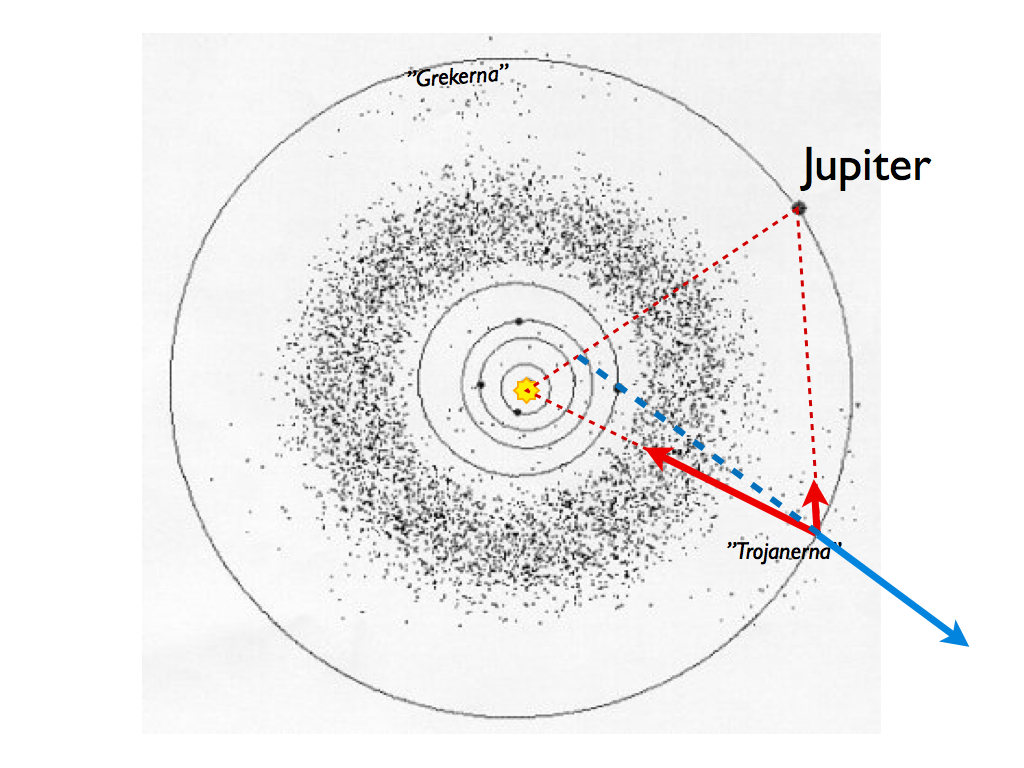

Bildtext: En asteroid i lagrangepunkterna L4 (grekerna) och L5 (trojanerna). De ligger 60 grader före och efter Jupiter. Asteroiden hålls på plats av en corioliseffekt som beror på ett samspel mellan två dragningskrafter (solens och Jupiters, röda pilar) samt asteriodens egen centrifugalkraft (blå pil).

Det som gör att detta hör hemma på Martins vädersajt är att den mekanism som håller fast asteroiderna vid L4 och L5 är corioliseffekten. Nej, det är inget skämt. Böcker om celest mekanik på typiskt 600 sidor brukar ägna 15-20 sidor åt att reda ut bara detta.Men ni som läst om corioliskraften nyligen på dessa sidor ska få en snabbförklaring:

Som ni vet handlar corioliskraften på jorden om balansen, eller obalansen, mellan två krafter: jordens dragningskraft (gravitationen) och centrifugalkraften av dess dagliga rotation. I lagrangepunkterna L4 och L5 handlar det om balansen eller obalansen mellan tre liknande krafter, dragningskrafterna från solen och Jupiter samt centrifugalkraften av asteroidens rotation runt solen.

Corioliseffekten skapar alltså förutsättningar för stabila och instabila jämviktslägen i mellan planeterna i vårt solsystem. Det är inte bara fascinerande att förstå fysiken med vilken man kan beskriva skeende och företeelser i världen. Det är mycket fascinerande att se att, och hur, samma fysikaliska lagar kan tillämpas inom vitt skilda områden.

Corioliseffekten fyller samma funktion i Largrangepunkterna L4 och L5 som den gör i atmosfären, dvs att ”hålla fast” föremål/luftpaket, göra det svårt för dem att röra sig fritt genom att, när de rör sig, söka få dem att återvända till utgångspunkten. Detta är avgörande för att förstå den allmänna cirkulationen. Jag återkommer.(!) / Anders Persson

PS: Man går aldrig säker för corioliseffekten. Strax före jul 1914 drabbade brittiska flottstyrkor samman med tyska utanför Falklandsöarna i södra Atlanten. Artilleristerna hade i över 80 år haft klart för sig att långskjutande kanoner måste ställas in också med hänsyn till corioliseffekten (och inte bara vind och lufttemperatur). Men eftersom britterna just hade anlänt från sina hemmabaser gällde deras korrektioner på norra halvklotet där corioliseffekten viker av artilleripjäserna till höger i stället för till vänster. Det var på vippen att tyskarna vann den bataljen, men britterna upptäckt sitt misstag precis i tid. DS.