Martin Hedberg:
Nedan följer en text skriven av Anders Persson om coriolieffekten. Anders är meteorolog och forskare knuten till ECMWF (The European Centre for Medium-Range Weather Forecasts). ECMWF är en oberoende internationell forskningsorganisation som finansieras av 34 nationer.
Anders beskriver hur den viktiga så kallade Corioliseffekten fungerar. Att han skriver just här just nu beror på att han nyligen råkade snubbla över en blogg jag skrev för något år sedan rörande corioliseffekten. Anders var inte helt tillfreds med de förenklingar jag gjort. Han påpekade det för mig och jag bjöd in honom att förklara corioliseffekten.
Corioliseffekten är grundläggande inom meteorologin och en förståelse av den hjälper oss att förstå hur kroppar (alltifrån havsströmmar till luft) rör sig under inverkan av olika krafter på ett roterande klot, dvs planeten Jorden.
Anders konstaterar att många förstår relativitetsteorin, men få förstår Corioliseffekten, trots att deras vetenskapliga beskrivningar är jämngamla. (Det första påståendet är jag inte helt överens med Anders om.)
Vad krävs det då för att man skall förstå corioliseffekten? Jo enligt Anders så behöver man först och främst förstå skillnaden mellan mellan dragningskraft och tyngdkraft (gravitation respektive gravity på engelska). Men han konstaterar också att de flesta, inklusive många professorer, inte förstår skillnaden vilket givetvis skapar problem.
Dragningskraften är riktad in mot jordens masscentrum. Tyngdkraften är summan av dragningskraften och centrifugalkraften. Den är orienterad vinkelrät mot jordens yta.
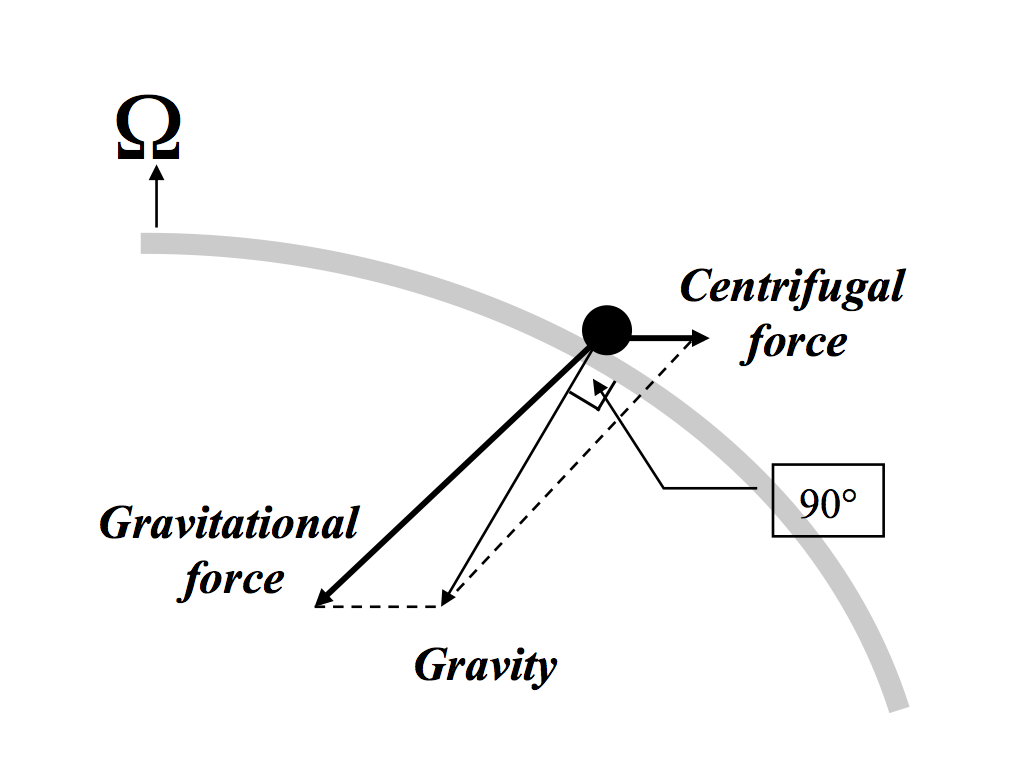
På grund av jordens rotation och den därav följda icke-sfäriska form kommer summan av dragningskraften g* och centrifugalkraften C att utgöra ett föremåls tyngd (g) vilken pekar ”rakt ner” (vinkelrätt mot en vattenyta i vila). Varje rörelse hos föremålet rubbar denna jämvikt och ger upphov till accelerationskomponenten horisontalt och vertikalt. Det är dessa som bla. är kända under benämningarna ”corioliseffekten” (horisontalt) och ”eötvöseffekten” (vertikalt). (Text och bild: Anders Persson)
Många vetenskapliga problem kan förstås genom att man förenklar och använder metaforer. Vi har också blivit bortskämda med många alldagliga förklaringar på komplicerade fenomen och fakta. Men kraven på enkla lösningar och strävan att förenkla för att förklara får inte gå för långt. Det finns en uppenbar risk att man förstår rätt, men av fel anledning. När man senare skall använda sin ”kunskap” i ett annat sammanhang kan bristerna bli både uppenbara och allvarliga.
Att i en blogg få med allt som rör corioliseffekten är svårt. Det finns därför ett par länkar i slutet av texten för den som vill fördjupa sig i ämnet.
God läsning, nu har ni något att sysselsätta er med medan lågtryck och högtryck avlöser varandra.
/Martin
Anders Persson:
Det som vetenskapsmän, matematiker och meteorologer är ense om och varit ense om i 150 mår är att den sk. corioliskraften, eller kanske rättare corioliseffekten påverkar ett föremål som rör sig friktionsfritt över jordytan på så sätt att rörelsen avlänkas vinkelrät mot rörelsen och proportionellt mot hastigheten. Detta har till följd att en partikel som friktionsfritt rör sig över jordytan dras in i en cirkelrörelse (för 10 m/s med knappt 100 km radie och omloppstid på 14 timmar).
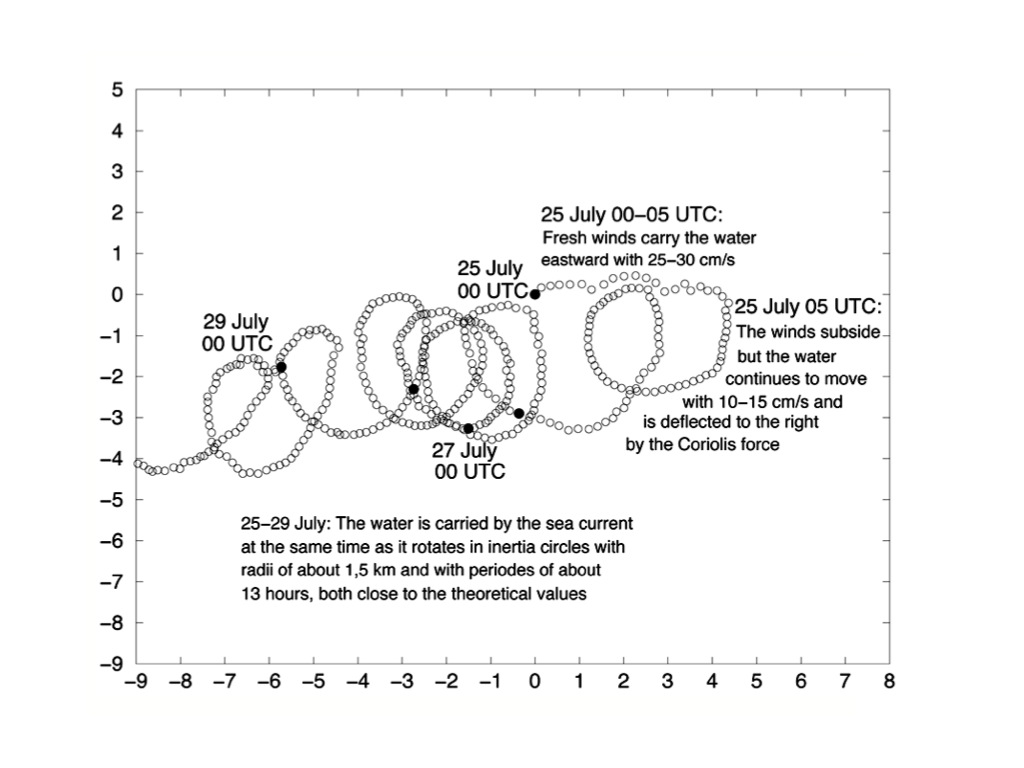
Rörelsen hos Östersjönsvattenmassor några sommardagar 1969 utanför Södertörn enligt mätningar som gjordes av Barry Broman på SMHI:s oceanografiska avdelning. En kort period av kraftiga vindar satte ytvattnet i rörelse. Sedan vinden bedarrat den 25 juli fortsatte vattenmassorna under några dagar att röra sig i tröghetscirklar som sakta drev i havsströmmen.
Fysikaliskt innebär detta att corioliseffekten har den fundamentala konsekvensen att det är svårt för luftmassor i atmosfären att förflytta sig några nämnvärda sträckor. Att de ändå förmår göra det är tack vare de starka horisontella krafter som byggs upp delvis tack vare atmosfärens täthets- och temperaturmotsättningar.
Så långt vad alla är ense om. Vad man diskuterat i 150 år är hur detta ska kunna förklaras intuitivt. En del menar att detta är omöjligt eftersom vi från vårt vardagsliv inte har någon erfarenhet av friktionsfri rörelse, minst av allt i ett roterande system. Andra menar att eftersom mycket annat (t.ex. Einsteins relativitetsteori) har kunnat förklaras lättbegripligt borde det ju det inte erbjuda något oöverstigligt hinder att förstå corioliseffekten intuitivt.
Problemet har dock under dessa 150 år varit den stora mängden ytterst ”lättförståeliga” men icke desto mindre felaktiga, vilseledande eller ofullständiga förklaringar. När Einstein 1905 i en tysk vetenskaplig tidskrift (Annalen der Physik) presenterade sina banbrytande uppsatser försiggick samtidigt i tidskriften en debatt om hur man skulle förstå corioliseffekten. Den bröt upp utan att man nått något resultat just därför att deltagarna var absolut övertygade om att vissa ”lättbegripliga” förklaringar måste vara riktiga ehuru de var svåra att sammanjämka med de matematiska ekvationerna.
Över 100 år senare begriper de flesta av oss Einsteins teorier, men famlar fortfarande i mörkret när det gäller corioliseffekten. Låt oss först ta tjuren vid hornen och identifiera de skenbart ”lättbegripliga” förklaringarna:
Den vanligaste är också den mest felaktiga, nämligen att avlänkningen beror på att luften rör sig över latituder med olika ostliga rörelser. Denna förklaring är 100% fel och det av flera orsaker, bl.a. att av denna förklaring följer att luften kommer att ändra sin hastighet högt avsevärt (motsvarande skillnaden i latituderna hastigheter). I verkligheten ändas inte luftens hastighet på grund av corioliseffekten.
Till de vilseledande hör de som betraktar en satellit i omloppsbana från pol till pol, alternativt en interkontinental missil som avfyras från någon as polerna. Denna förklaring är inte fel men eftersom hastigheten är 100-tals gånger större än vad luften blåser i atmosfären bryter matematiken kring ”tröghetscirkeln” mer eller mindre samman. Den intuitiva förståelse man får genom satelliter och missiler duger kanske för att förstå deras avlänkning, men inte luftens eller havsströmmarnas.
Till sist har vi två personer som kastar bollar till varandra medan de snurrar runt på en karusell. En något enklare version är golfspelaren som gör en putt på en stor snurrande karusell. För någon som står bredvid karusellen verkar bollen gå rakt, för golfspelaren verkar den vika av (åt höger om karusellen roterar moturs, som jorden). Denna förklaring är ofullständig eftersom det inte görs klart att vi har ytterligare en effekt verksam nämligen centrifugalkraften. Den gör att golfbollen, ur spelarens synvinkel gradvis försvinner ur sikte i en sig ständigt utvidgande spiral och aldrig kommer tillbaka. Om vi antar att bollen rör sig med 10 m/s och karusellen har en omloppstid på 5 sekunder skulle bollen, om bara corioliseffekten var verksam, snurra runt i en cirkel på 4 meters radie, dvs om centrifugaleffekten inte var närvarande.
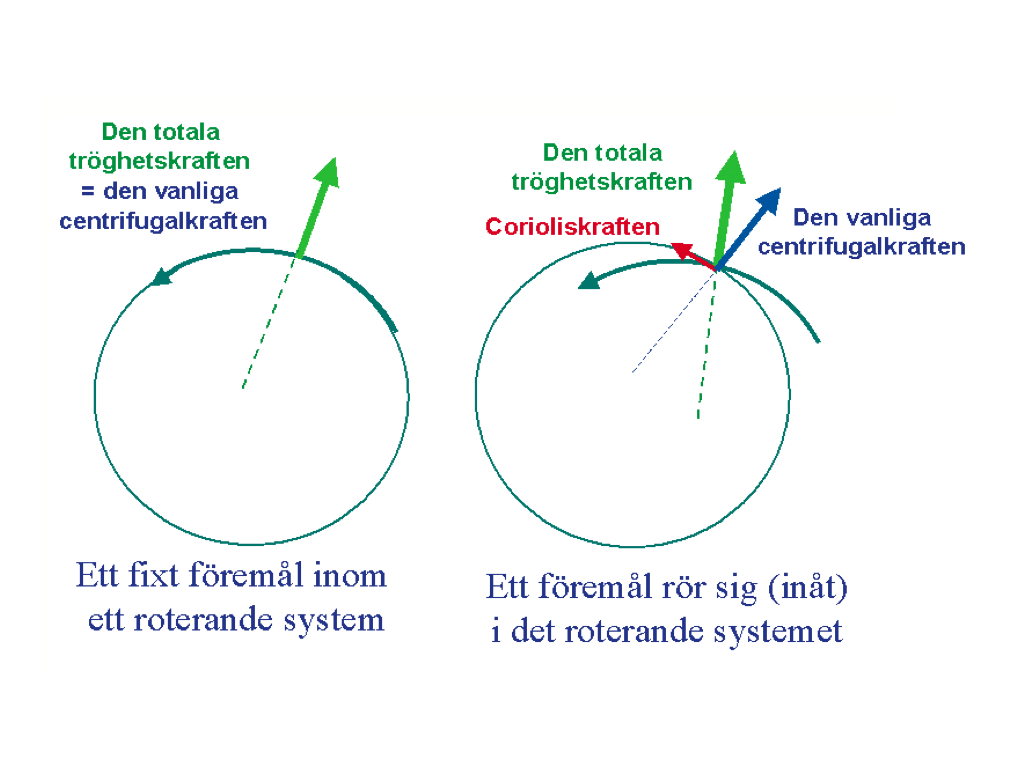
Gaspard Gustave Coriolis fann 1835 att ett föremål som rörde sig inom och relativt ett roterande system erhöll en total tröghetseffekt som var lika med vektorsumman av den normala centrifugalkraften plus en (ofta mindre) tröghetskraft, det som kom att bära hans namn.
Ett sätt att göra sig kvitt centrifugaleffekten, neutralisera eller balansera den, är att deformera karusellen, göra den till en något konkav parabol. Den utåtriktade centrifugalkraften skulle då balanseras eller neutraliseras av tyngdkraften som vill dra bollen neråt, men samtidigt inåt, på grund av inverkan av karusellväggens parabolform.
Samma mekanism, fast ”upp och ner”, är hemligheten bakom corioliseffekten på jordytan (eller varje snurrande planet). Vår jord snurrar som bekant och den därav följande centrifugaleffekten har utvidgat jorden kring ekvatorn, plattat till den vid polerna på ett sätt som gör att den utåtriktade centrifugalkraften exakt balanseras av jordens dragningskraft (gravitation) som inte pekar rakt ”neråt” utan en aning inåt, mot jordaxeln. Vad som pekar ”rakt ner” är jordens tyngdkraft, vilken är summan av dragningskraften och centrifugalkraften.
Men denna balans finns bara så länge vi står still. Rör vi oss påverkas inte dragningskraften, men väl centrifugalkraften. Om vi för enkelhetens skull antar att vi springer österut så ökar vår totala ostliga rörelse och därmed den utåtriktade centrifugalkraften. Ökningen är vinkelrät mot rörelsen och pekar åt höger. Springer vi västerut minskar centrifugalkraften, den komponent av jordens dragningskraft som pekar inåt får övertaget och avlänkningen sker återigen åt höger.
Man kan på liknande sätt, utifrån en diskussion av obalansen mellan jordens dragningskraft och centrifugalkraft bevisa samma sak för nord-sydlig rörelse. Det är dock lite bökigare och den intresserade hänvisas till sidan 15 i en artikel jag skrev för flera år sedan och som nu hittas på många ställen på nätet, bla. på Princetonuniversitetets: http://www.aos.princeton.edu/WWWPUBLIC/gkv/history/persson_on_coriolis05.pdf
Den intresserade läsaren hänvisas också till http://www.meteohistory.org/2006historyofmeteorology3/2persson_hadley.pdf
God fortsättning önskar
/Anders Persson, meteorolog ECMWF