Häromdagen gjorde jag en intervju för en kvällstidning. Jag hörde hur journalisten fiskade efter något som ”stack ut” lite. Vis av erfarenheten höll jag igen. Jag vet nämligen allt för väl hur en liten kommentar i en bisats lätt kan bli såväl rubrik som löpsedel. Det är i och för sig inte journalistens ”fel” utan snarare den personen som sätter rubrikerna.
Men det finns också något mer grundläggande i systemet som gör att man som sakkunnig ofta känner att det blir lite väl hård vinkel på ens yttrande. Medias roll är nämligen inte att bara ge den breda bilden. Minst lika ofta handlar det om att finna extremer. Det är inte bara för att kunna sälja lösnummer, nej det är minst lika viktigt för att det är extremerna i sig som är viktiga.
När vi meteorologer blir intervjuade på temat ”vädret kommande dagar” så fokuserar jag på det som de flesta kommer att uppleva. Om det skulle vara något extremt som kan betraktas som ”samhällsfarligt” så tar jag givetvis med det också. Men om det är något pseudo-extremt som en dag med solsken efter en vecka med mulet väder, eller svaret på frågan om var man hittar det ”bästa” vädret, då passar jag.
Utöver det så går det inte att beräkna vädret exakt. Men eftersom prognoserna (även de vi publicerar på Klart) anger ett tal för såväl temperatur som vindar och nederbörd så upplevs de som mycket precisa. Men vi vet att det handlar om sannolikheter för det ena eller andra. Det gäller såväl i tid som i rum.
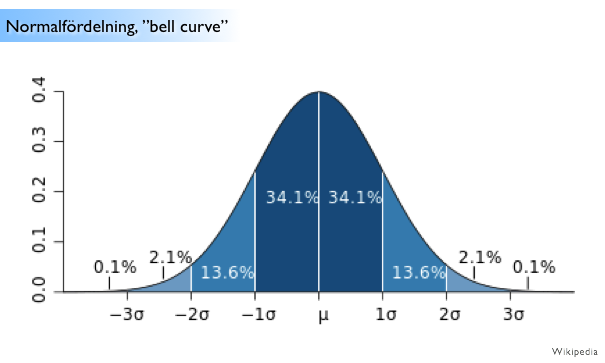”Normalfördelning”. Låter krånglig, men det går bra att läsa resten av artikeln utan att greppa alla detaljer i matematiken 🙂
Bättre vore att ha ett intervall. Ovan ser ni en graf som visar en så kallad ”normalfördelning”. Den speglar verkligheten avsevärt mycket bättre. På y-axeln anges sannolikheten för att något av värdena på x-axeln skall inträffa. Det kan vara mycket skilda saker som tex: bränsleförbrukningen i din bil, antal sidor i en pocketbok, tidpunkten då äppelträdet blommar, temperaturen på midsommarafton, lufttrycket i Skövde osv.
Standardavvikelsen, σ (sigma), är ett mått på hur mycket de enskilda värdena, tex temperaturen på en enskild plats, avviker från medelvärdet (μ) av temperaturerna. Tex finner man knappt 70% av de enskilda fallen inom ± 1 standardavvikelse. Går man ut till två standardavvikelser så finner man 95% av observationerna.
Vad vill jag säga med detta? Jo ett par saker:
- Ibland befinner sig våra prognoser, i synnerhet de långa prognoserna, i ytterkanten av normalfördelningskurvan. Jag vill då försöka ”dra in” dem mot mitten för att bättre representera verkligheten.
- Jag strävar efter att inte bara presentera ett värde (tex medelvärdet μ) av vädret, utan snarare ett intervall. Genom att visa intervallet ±1,5 σ så får man en bra representation av den verklighet som de flesta kommer att uppleva. (Det blir dock lätt ”rörigt” rent grafiskt om man skall göra detta på webben eller i mobiltelefon.)
- Journalister och i synnerhet rubriksättare är mest intresserade av det som ligger i ytterkanterna. Om det kan bli översvämning någonstans så säger jag ”Det skulle kunna bli översvämning någonstans”. Men rubriken/löpsedeln blir istället ”VÄDERKAOS: ÖVERSVÄMNINGAR!”. Eller om det generellt blir mellan 20 och 25 grader, lokalt lite varmare så blir rubriken: ”SOMMARSMOCKA +30”.
- Ett dilemma är att det ofta är extrempunkterna som verkligen är viktiga. De som drabbas av översvämningar drabbas hårt. Men vänder man kameran åt andra hållet så är det bara blött i gräset. Det genomförs miljontals flygningar varje år, men enstaka flygkrascher gör att folk är räddare för att flyga än att köra bil. Det är som med lotteri: Sannolikheten för att vinna är en på flera miljoner, ändå tror folk att turen skall drabba just dem. Det händer att man får en skev bild av verkligheten genom media (och marknadsförare). Men den som drabbas av det extrema påverkas givetvis väldigt mycket.
- Risken med en sån här belysning är att folk tror att media ALLTID ger en skev bild. Det gör de givetvis inte. Det jag vill säga är att man skall läsa kritiskt. Framför allt skall man läsa löptexten och inte bara rubrikerna. Ju längre från källan desto större sannolikhet för att fakta är vinklat, förvanskat eller i alla fall kraftigt förenklat med en dragning åt det extrema och spektakulära.
/Martin